An AI just entered a fifty-year-old mathematical race, and it's winning in ways no one expected.
In 1969, a German mathematician named Volker Strassen made a discovery that shook the mathematics world. For centuries, everyone multiplied matrices the same straightforward way. A simple operation requiring eight scalar multiplications for two-by-two matrices.
Then Strassen proved everyone was wrong. With some clever algebraic rearrangement, he cut that number down to seven. Fifty years passed. No human mathematician beat him.
Then, in October 2022, something unexpected happened. DeepMind introduced AlphaTensor, a reinforcement learning system designed to discover novel, efficient, and provably correct algorithms for fundamental mathematical operations.
Unlike the slow crawl of human progress, AlphaTensor found algorithms that outperformed state-of-the-art solutions for many matrix sizes. For 4 by 4 matrices specifically, it achieved a 47-step solution while Strassen's required 49 steps.
This isn't simply a win for computer science. It represents something deeper: a glimpse into how machines can explore mathematical territory that humans have left untouched for decades.
Why Matrix Multiplication Actually Matters
Before diving into AlphaTensor's genius, understanding why anyone cares about multiplying matrices faster is essential.
Matrix multiplication is everywhere. It's the operation your smartphone uses to process images. It's the foundation of speech recognition systems. It powers the graphics rendering in video games.
It runs the simulations that predict weather patterns. Behind nearly every neural network powering modern artificial intelligence, matrix multiplication is doing the heavy computational lifting.
Consider the fundamental operation: when multiplying two n×n matrices A and B to produce result C, the standard algorithm performs the following computation:
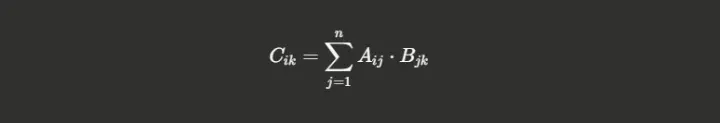
This requires n³ scalar multiplications. For a 1000×1000 matrix, that's one billion operations. When you're training a massive language model or processing billions of images, saving even a few percentage points per multiplication compounds into massive real-world gains.
Discovered algorithms have multiplied large matrices between 10 and 20 percent faster than commonly used algorithms on the same hardware. That seemingly small percentage translates to hours of computation saved across Google's data centers and research institutions worldwide.
For decades, mathematicians assumed they'd discovered near-optimal solutions. They were wrong. They'd only scratched the surface of what was possible.
The Game That Changed Everything
Here's where AlphaTensor becomes genuinely clever. Rather than asking mathematicians to stare at equations until inspiration struck, DeepMind framed the entire problem as a game. Not chess or Go, but something mathematicians would instantly recognize: a tensor decomposition puzzle.
The problem formulation uses tensor representation. A matrix multiplication operation can be expressed as a 3-way tensor T where we seek the minimal rank decomposition:
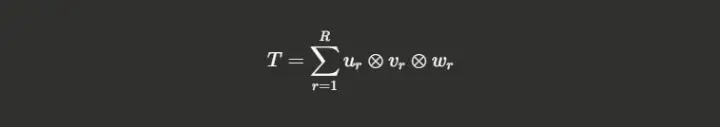
Here, R represents the rank, which directly corresponds to the number of scalar multiplications needed. The subscripts u, v, and w represent linear combinations of the matrix indices. Finding algorithms means finding decompositions with the smallest possible rank.
Imagine you have a three-dimensional block of numbers that represents everything wrong about your current multiplication approach. Your job is to break it down piece by piece until nothing remains.
Each move you make, each decomposition step you take, is actually a mathematical operation. When you finish the game, you've inadvertently invented a multiplication algorithm.
The complexity is staggering. The branching factor at each step is over 10³³. This dwarfs the challenge of Go, a game that once seemed unsolvable for artificial intelligence. Most game-playing AI systems would collapse under this complexity. AlphaTensor wasn't ordinary.
Building on Giants: From AlphaZero to AlphaTensor
AlphaTensor builds directly upon AlphaZero, the AI system that achieved superhuman mastery of chess and Go using deep reinforcement learning and Monte Carlo tree search. Both systems learn through self-play, receiving feedback from their own moves, adjusting strategy incrementally, and gradually improving their approach.
The innovation lies in the neural network architecture itself. The researchers didn't simply copy AlphaZero's design. They built something new. A neural network that understands the algebraic structure of tensors, that recognizes when symmetries matter, that sees when two apparently different moves are essentially identical.
They developed novel components including a specialized neural network architecture incorporating problem-specific inductive biases, a procedure to generate useful synthetic training data, and a method to leverage the mathematical symmetries inherent in the problem.
The reward function for AlphaTensor uses a carefully designed structure:
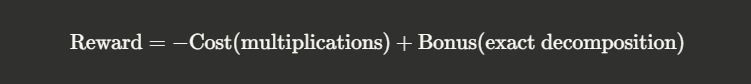
AlphaTensor started with zero knowledge about existing matrix multiplication algorithms. It didn't know about Strassen. It didn't understand the standard textbook method. It knew only this: reduce this tensor to zero, minimize the number of moves, and check if you've achieved the goal.
By playing this game billions of times against itself, it discovered patterns humans had never seen.
What AlphaTensor Actually Discovered
Headlines focused on the obvious victory: breaking Strassen's fifty-year record for 4 by 4 matrices. The actual discovery was far richer and more interesting.
AlphaTensor discovered over 14,000 nonequivalent algorithms for matrix multiplication, revealing that the entire space of possible algorithms is vastly richer than anyone had suspected. This is the genuine insight. Mathematicians had believed they'd nearly exhausted the possibilities. AlphaTensor demonstrated they'd barely begun.
For different matrix sizes, different hardware architectures, and different mathematical fields, entirely different optimal solutions existed. Solutions no human had ever found because they were hidden in a combinatorial space so enormous that traditional human-guided search was fundamentally impossible.
When you use an algorithm recursively to multiply larger matrices, the complexity scales according to:
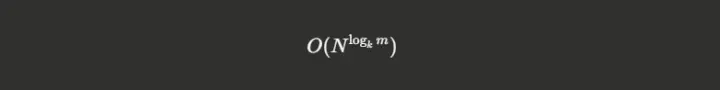
Where k is the dimension (for 4×4 matrices, k=4) and m is the number of multiplications in the base case. Strassen's algorithm achieves approximately N^2.81, while new 47-multiplication algorithms achieve approximately N^2.7986, a meaningful improvement across massive matrix multiplications.
For practical applications, the gains remain modest but real. When AlphaTensor's algorithms were optimized for specific hardware, they delivered measurable speedups. Benchmarks showed improvements of up to 16 percent on NVIDIA V100 GPUs and 22 percent on Tesla T4 chips, particularly for large matrices around 18,000 dimensions.
These aren't purely theoretical wins. These are actual seconds saved on real computers doing real work.
Why Verification Matters More Than Speed
Here's something that separates AlphaTensor from other AI breakthroughs: everything it discovered is provably correct.
When you discover a matrix multiplication algorithm through random search or neural network suggestions, you need absolute certainty it actually works. A fast incorrect algorithm is worthless. Every discovered algorithm corresponds to an exact algebraic identity. You can verify it through symbolic expansion and tensor equality, ensuring provable correctness despite relying on reinforcement learning search.
The verification process confirms that for any decomposition, the following holds true:
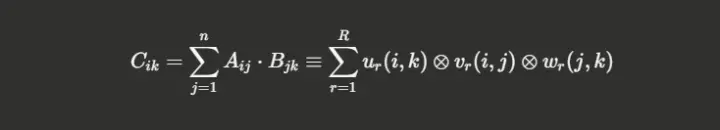
This distinction matters profoundly. AlphaTensor's discoveries aren't mysterious black boxes. You can take any algorithm it found, expand the algebra, and mathematically prove it computes matrix multiplication correctly. It's like discovering treasure with a certificate of authenticity included.
The Reality Check: Theory Versus Practice
But here's where genuine complexity emerges. The mathematics community approached AlphaTensor's discoveries with thoughtful skepticism.
The new 47-step algorithm works only in finite fields, not over real numbers. The fundamental question haunting researchers for decades remains unanswered. Whether there exists a fundamentally faster way to multiply arbitrarily large matrices is still unknown. The improvements discovered by AlphaTensor don't represent a major breakthrough for the general problem of complexity.
The space is richer than previously known, but the deepest questions remain open. Some researchers saw this as tempering the excitement. Others recognized it as exactly what you'd expect: AI excels at finding improvements in bounded, specific domains. Theoretical questions still require human mathematicians and rigorous proof.
What's actually remarkable is how the collaboration unfolded. Within days of AlphaTensor's publication, mathematicians used its discoveries as jumping-off points and found even better algorithms themselves. The machine didn't replace human insight. It expanded the landscape of possibilities humans could explore.
The Bigger Picture: Automated Discovery
AlphaTensor proves that reinforcement learning can systematically search combinatorial spaces that seem impossible to explore and find novel, correct, practical solutions.
If you can frame another mathematical problem as a game, whether polynomial multiplication or quantum circuit optimization, you could potentially apply similar techniques to explore spaces humans cannot access using neural networks guided by Monte Carlo tree search.
This represents a genuine shift in how we approach hard algorithmic problems. The race that started with Strassen in 1969 suddenly looks different. The finish line isn't just faster algorithms anymore. It's discovering a new methodology for finding them.
And we're probably just getting started.